比特差错检测和纠正技术
数据在链路层传输时,比特差错是一个无法回避的问题。当比特差错发生之后我们如何检测和纠正呢?本文主要介绍检测比特差错的基本思想和三种实现技术,它们分别是:奇偶校验、校验和、循环冗余检测。
如何发现比特差错
如图 5-3 所示,左侧的发送结点为了保护数据比特,使用差错检测和纠正比特(Error-Detection and-Correction, EDC)来增强数据 D。要保护的数据不仅包括从网络层传递下来的数据报(Datagram),还包括链路层帧(Frame)首部中的 MAC 地址、以太类型等字段。链路层的 D 和 EDC 都被发送到接收结点,右侧的接收结点接收到比特序列 D’ 和 EDC’。由于传输中可能会发生比特翻转(由 0 变成 1 或 由 1 变成 0),所以 D’ 和 EDC’ 可能与 D 和 EDC 不同。
图 5-3 差错检测与纠正场景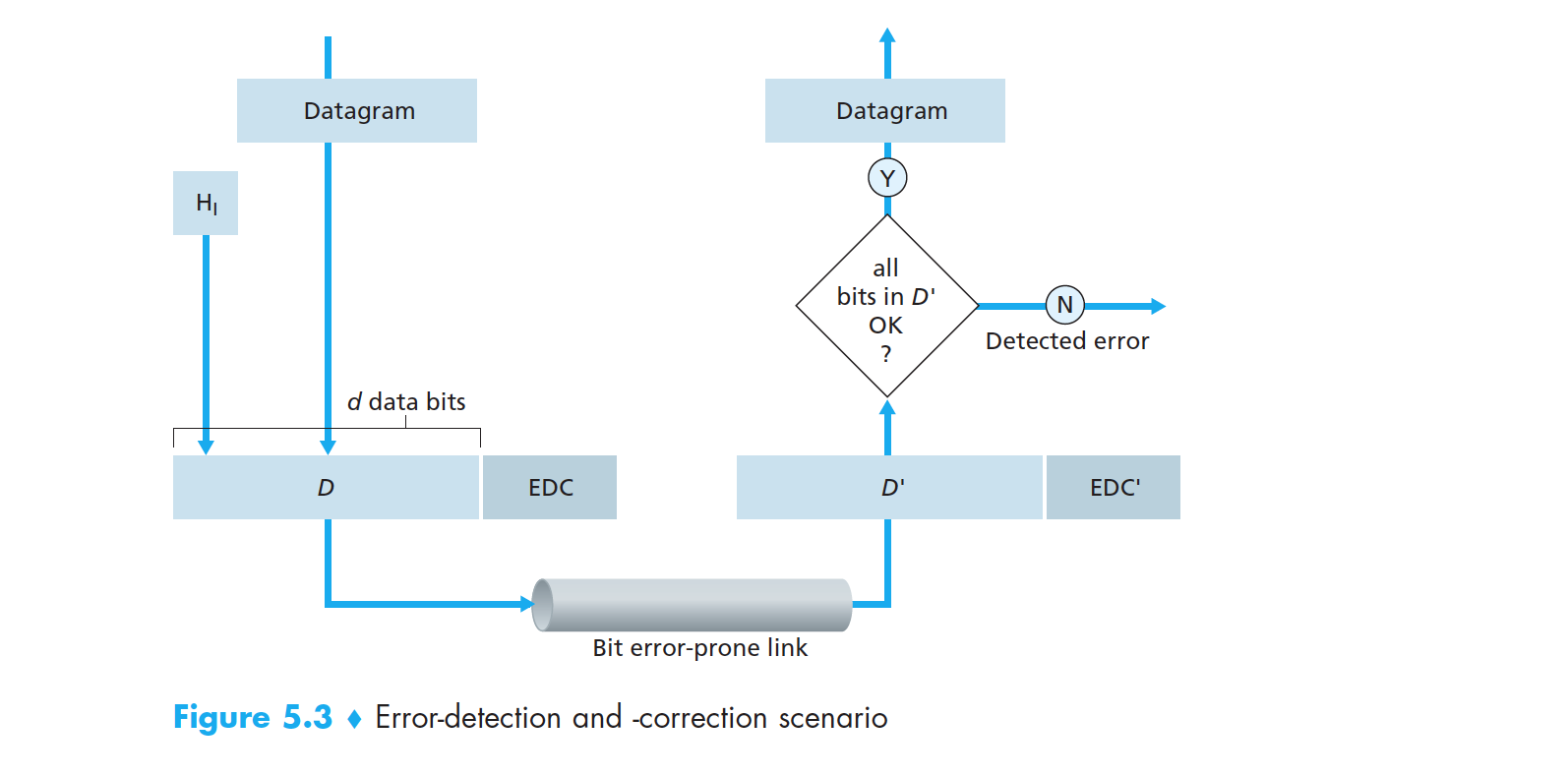
接收方的挑战是在它只收到 D’ 和 EDC’ 的情况下,如何确定 D’ 是否和初始的 D 相同。差错检测和纠正技术使接收方有时(并非总是)检测出比特差错。也就是说,接收方可能无法知道接收的信息中包含比特差错,从而向网络层交付一个受损的数据报。
因此,我们需要选择一个使这种事件发生的概率更低的差错检测方案。一般来说,差错检测和纠错技术越复杂,发生的概率就越低,但同时开销就越大(这意味着需要更多的计算和更多的差错检测和纠正比特)。
奇偶校验(Parity Checks)
检测
最简单的差错检测就是用单个奇偶校验位(parity bit)。假设要发送的信息 D 有 d 个比特。在偶校验方案中,发送方只需要包含一个附加的比特(即校验比特)并选择它的值,使得这 d+1 个比特中有偶数个 1。同理,在奇校验方案中,选择校验比特值使得有奇数个 1。图 5-4 就描述了一个偶校验方案,校验比特被存放在一个单独的字段中。
图 5-4 一比特位的偶校验
采用单个奇偶校验位的方式,接收方的操作也很简单。接收方只需要数一数 d+1 比特中 1 的数量即可。如果在采用偶校验方案中发现了奇数个值为 1 的比特,接收方就知道至少出现了一个比特差错(更精确的说法是,出现了奇数个比特差错)。
未检测出的比特差错
当出现了偶数个比特差错,会发生什么现象呢?这将导致一个未检测出的差错。如果发生比特差错的概率小,而且比特之间的差错可看作是独立发生的,那么在同一个分组中出现多个比特差错的概率将是极小的。在这种情况下,单个奇偶校验位可能足够了。但是,现实场景中差错经常以突发的方式聚集在一起,而不是独立的发生。在突发差错的情况下,使用单比特奇偶校验保护的一组数据中未检测出差错的概率是 50%。 显然,我们需要一个更加健壮的差错检测方案。
纠错
在检测出存在比特差错之后应该如何纠错呢?我们以单比特奇偶校验方案为例,图 5-5 显示了单比特奇偶校验方案的二维实现。数据 D 中的 d 个比特被划分为 i 行 j 列。对每行和每列计算奇偶值。产生的 i+j+1 奇偶比特构成了链路层帧的差错检测比特。
图 5-5 二维偶校验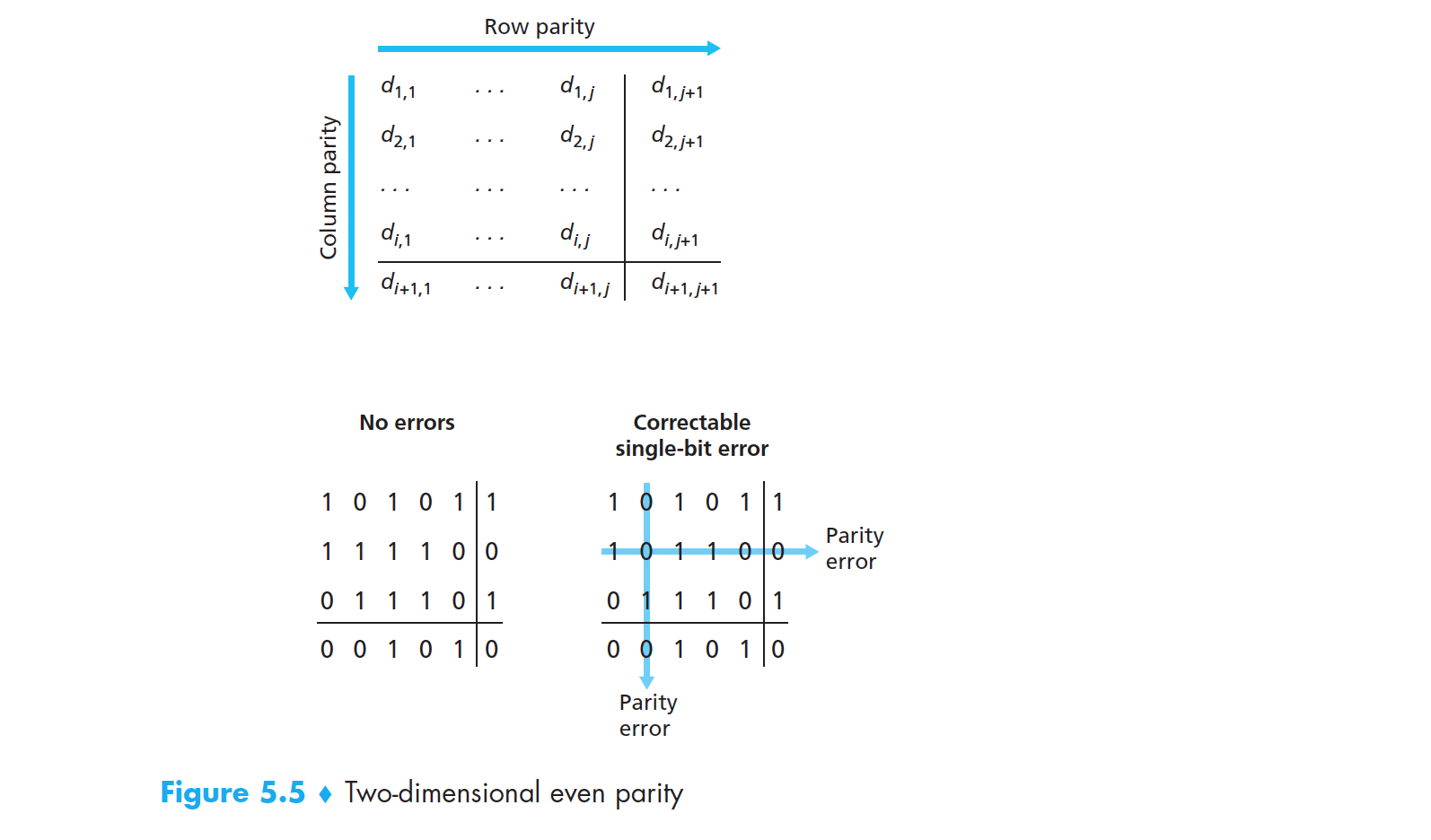
现在假设在初始 d 比特信息中出现了单个比特差错。使用这种二维奇偶校验(two-dimensional parity)方案,包含差错比特的行和列的校验值都会出现差错。因此,接收方不仅可以检测到发生了单个比特差错,而且可以利用行和列的索引来定位差错比特并纠正它!
接收方检测和纠正差错的能力被称为前向纠错(Forward Error Correction, FEC)。这些技术通常用于像音频 CD 这样的存储和回放设备中。FEC 技术很有价值,因为它们可以减少发送方重发的次数。更重要的是,它们允许在接收方立即纠正差错。FEC 能避免一些往返时延,这些时延是发送方收到 NAK 分组并向接收方重传数据时所花费的,这对于实时网络应用或具有长传播时延的链路来说是一种非常重要的优点。
校验和(Checksum)
因特网校验和
在检验和技术中, 图 5-4 中的 d 比特数据被视为一个 k 比特的整数序列。一个简单的检验和方法就是将这 k 比特整数加起来,并用得到的和作为差错检测比特。因特网检验和 就基于这种方法,将每 2 字节的数据视作 16 比特的整数并求和,这个和的反码就是首部的检验和字段(Header checksum)。
下图 IPv4 数据报的首部中就存在着一个 16 bit 的校验和字段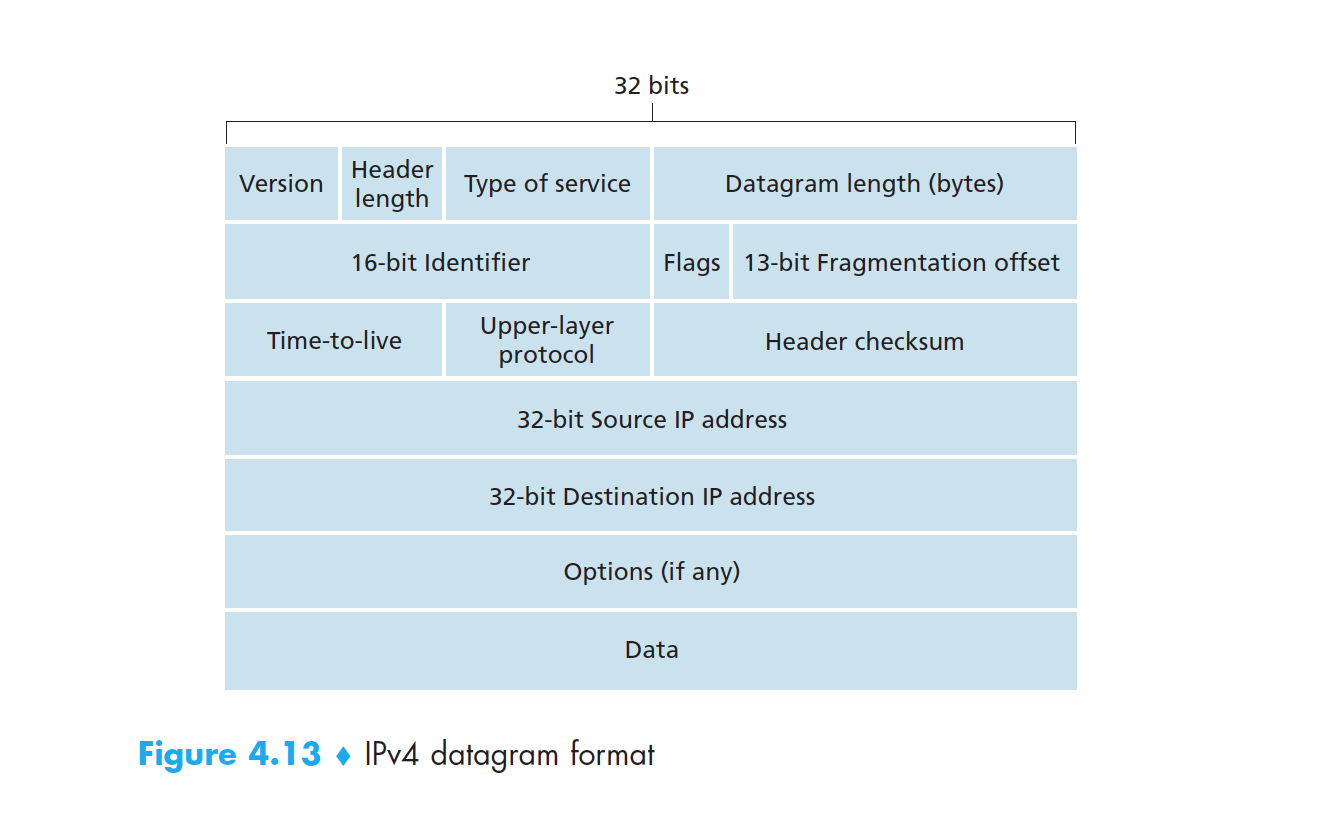
举个例子
发送方
假设一个 20 字节的 IPv4 首部数据如下(采用 16 进制表示),加粗的为校验和字段。
4500 0073 0000 4000 4011 b861 c0a8 0001 c0a8 00c7
(1) 跳过校验和字段,我们计算首部中每个 16 位值的总和。
4500 + 0073 + 0000 + 4000 + 4011 + c0a8 + 0001 + c0a8 + 00c7 = 2479c
(2) 我们将 2479c 转换为二进制。
0010 0100 0111 1001 1100
(3) 前 4 位是进位,我们将其加到最低位。
(0010) + (0100 0111 1001 1100) = 0100 0111 1001 1110
(4) 在这个例子中,加完进位之后不产生新的进位。如果有的话,重复第 3 步。
(5) 接下来,我们将该值中的每一位取反,以获得校验和。
0100 0111 1001 1110
变为
1011 1000 0110 0001
用十六进制来表示即为 b861,如前面加粗部分所示。
接收方
在验证校验和时,使用与上述相同的过程,只是原始校验和字段不跳过。
(1) 4500 + 0073 + 0000 + 4000 + 4011 + b861 + c0a8 + 0001 + c0a8 + 00c7 = 2fffd
(2) 加上进位。
fffd + 2 = ffff
(3) 翻转每一位得到 0000,这表明没有检测到差错(注意,IP 首部校验和无法检测 16 位值的正确顺序)。
应用场景
检验和方法适用于需要分组开销小的场景。TCP 和 UDP 中的检验和只用了 16 比特,与常用于链路层的 CRC 相比,它们提供相对弱的差错保护。
为什么传输层使用检验和而链路层使用 CRC 呢?因为传输层作为用户操作系统的一部分,通常是用软件来实现的,更适合采用简单而快速(如检验和)的差错检测方案。而链路层的差错检测是用硬件来实现的,它能够快速执行更复杂的 CRC 运算。
循环冗余检测(Cyclic Redundancy Check)
多项式编码
循环冗余检测(Cyclic Redundancy Check, CRC)也称为多项式编码(polynomial code),该编码将待发送的比特串看作是系数为 0 和 1 的一个多项式,对比特串的操作被解释为多项式运算。CRC 编码的思想如下:
- 数据 D 有 d 比特,发送方要将它发送给接收方。
- 发送方和接收方首先协商一个 r+1 比特串,称为生成多项式。我们将其表示为 G,同时规定 G 的最高有效位是 1。
- 对于数据 D,发送方要选择 r 个附加比特 R,并将 R 附加到 D 上。使得到的 d+r 比特数据(一个二进制数)用 模 2 运算 恰好能被 G 整除(即余数为 0)。
图 5-6 crc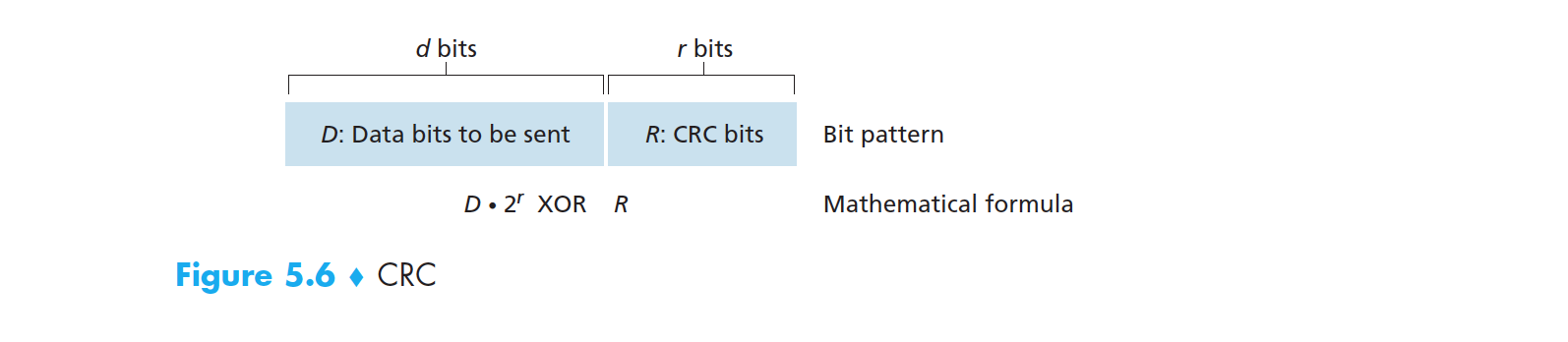
接收方用 CRC 进行差错检测的过程很简单:直接用 G 去除接收到的 d+r 比特。如果余数为非零,则出现了差错;否则认为数据正确。
所有 CRC 计算采用模 2 运算来做(在加法中不进位,在减法中不借位)。这意味着加法和减法是相同的,这两种操作等价于按位异或(XOR)。
举个例子
图 5-7 一个例子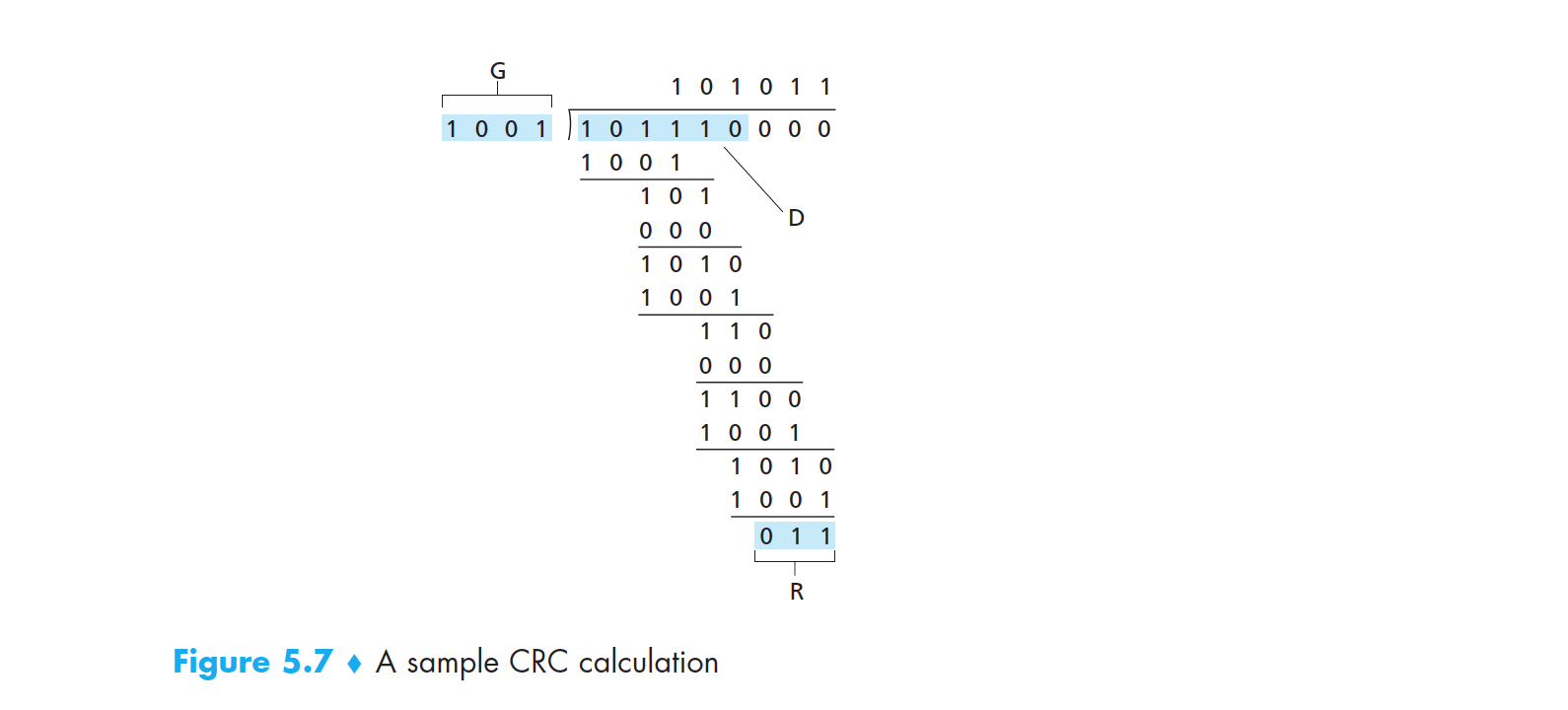
最终求出来的 R 将会被补充到待发送数据 D 的后面。发送方实际要发送的是 D+R,即 101110011。
小结
这些比特差错检测和纠正技术,正是我们能在网络中正确传递消息的基石。