数据压缩能够实现是因为多数现实世界的数据都有冗余。无损数据压缩通常利用了统计冗余,这样就能更加简练地、但仍然完整地表示发送方的数据,如行程长度编码(Run-length encoding)、霍夫曼编码(Huffman coding)。而在很多情况下,数据会包含比必要的还多的信息。例如,一张分辨率过高的照片,其中的细节肉眼可能已无法识别。若舍弃这些人类无法察觉的细节,就可以用更小的数据量来提供与原始数据相差无几的感官体验,这属于有损压缩。
数据压缩
无损和有损
压缩可以分为无损压缩和有损压缩。
- 无损,无损压缩适用于必须完整还原原始信息的场合。例如,文本、可执行文件、源代码等。
- 有损,指的是压缩之后就无法完整还原原始信息,但压缩比可以很高。主要应用于视频、音频等数据的压缩,因为损失了一点信息,人是很难察觉的。或者说,没那么清晰照样可以看可以听。
ZIP 格式
背景
ZIP 文件格式是一种数据压缩和文档储存的文件格式,原名 Deflate,发明者为菲尔·卡茨(Phil Katz,1962 年 11 月 3 日-2000 年 4 月 14 日),他于 1989 年 1 月公布了该格式的资料。ZIP 通常使用后缀名『.zip』,它的 MIME 格式为 application/zip。目前,ZIP 格式属于主流的压缩格式之一,其竞争者包括 RAR 格式以及开源的 7z 格式。
Microsoft 从 Windows ME 操作系统开始内置对 zip 格式的支持,即使用户的电脑上没有安装解压缩软件,也能打开和制作 zip 格式的压缩文件,OS X 和流行的 Linux 操作系统也对 zip 格式提供了类似的支持。因此如果在网络上传播和分发文件,zip 格式往往是最常用的选择。
1985 年一家名为 SEA(System Enhancement Associates)的小公司开发了一个在 MS-DOS 平台下的商业压缩软件,名为 ARC。当时的软件发行方式与现在略有不同,用户购买了软件,除了得到软件的可执行文件还包括一份 C 语言的源代码。当时的菲尔·卡茨与很多用计算机的平民一样,缺乏资金购买大量的商业软件,当时卡茨从网上下载了一份 ARC 的 C 语言源代码,并用汇编语言将其全新编写并编译出来。卡茨将这个软件名为:PKARC(Phillip Katz’ ARC)。
卡茨制作的新软件 PKARC 因为是参照源代码编写的,所以完全兼容 ARC 并且性能上比 ARC 高。卡茨当时将这个新软件上传到网络上面。显然,卡茨此举造成对 SEA 公司的侵权。SEA 最初希望通过联络卡茨使 PKARC 成为 SEA 公司旗下的一款产品,后来卡茨拒绝了。最终,双方对簿公堂,结果是卡茨败诉,卡茨被判以对 SEA 公司的赔款以及停止发放 PKARC。
后来,卡茨在研发过程中的 PKARC 续作也被迫重新改写所有代码,PKARC 其实就是 PKZIP 的前身,但卡茨没有从 PKARC 赚到一分钱,还是穷困潦倒,又因为酗酒等众多原因,2000 年死在一个汽车旅馆中。
文件头
现在使用任何一种文本编辑器打开 Zip 文件,都能看到前两个字母为 PK。对应的 16 进制编码为 50 4B。jar 包文件的开头也是 PK。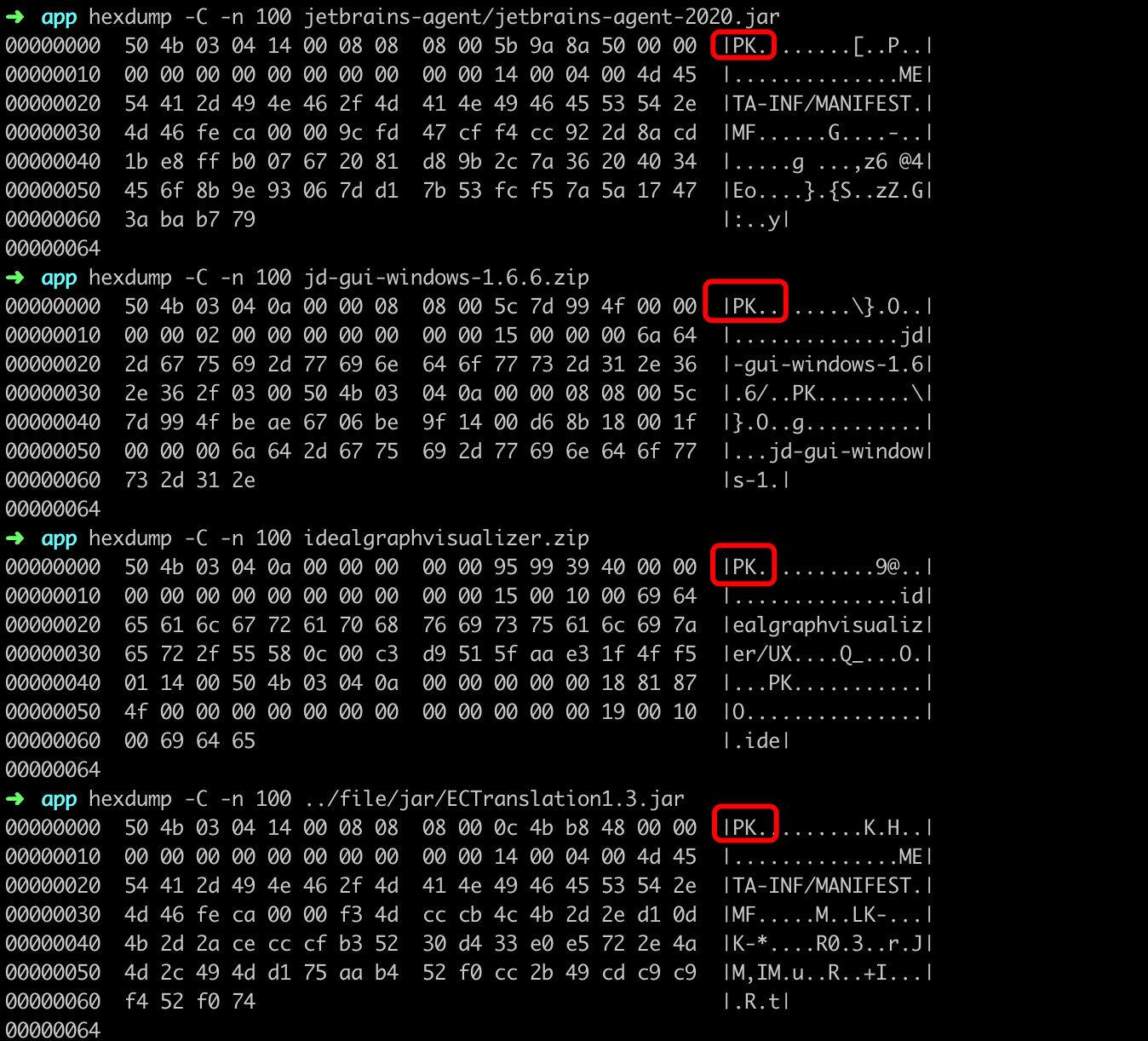
霍夫曼编码
霍夫曼编码使用变长编码表对源符号(例如,字母)进行编码,其中变长编码表是通过评估源符号出现的几率得到的。出现几率高的字母使用较短的编码,出现几率低的字母使用较长的编码,这使得编码之后字符串的总长度降低,从而达到无损压缩数据的目的。
前缀编码
假设我们要传输的字符为:ABACCDA
若编码为:
A-0
C-1
B-00
D-01
则编码后为:000011010
当我们对它进行解码的时候,会发现 0000 可能对应多种解码方式。如 AAAA、AAB、ABA、BB。所以,我们在设计长度不等的编码时,一定注意不能有重码的情况,即任意字符的编码不能是其它字符编码的前缀。这种编码方式就叫做前缀编码。
霍夫曼树
霍夫曼编码就是一种前缀编码,而且是最优前缀编码。想要获得霍夫曼编码,首先需要构建一颗霍夫曼树。
构建霍夫曼树的口诀
- 构造森林全是根
- 选用两小造新树
- 删除两小添新人
- 重复 2、3 剩单根
示例 1
霍夫曼编码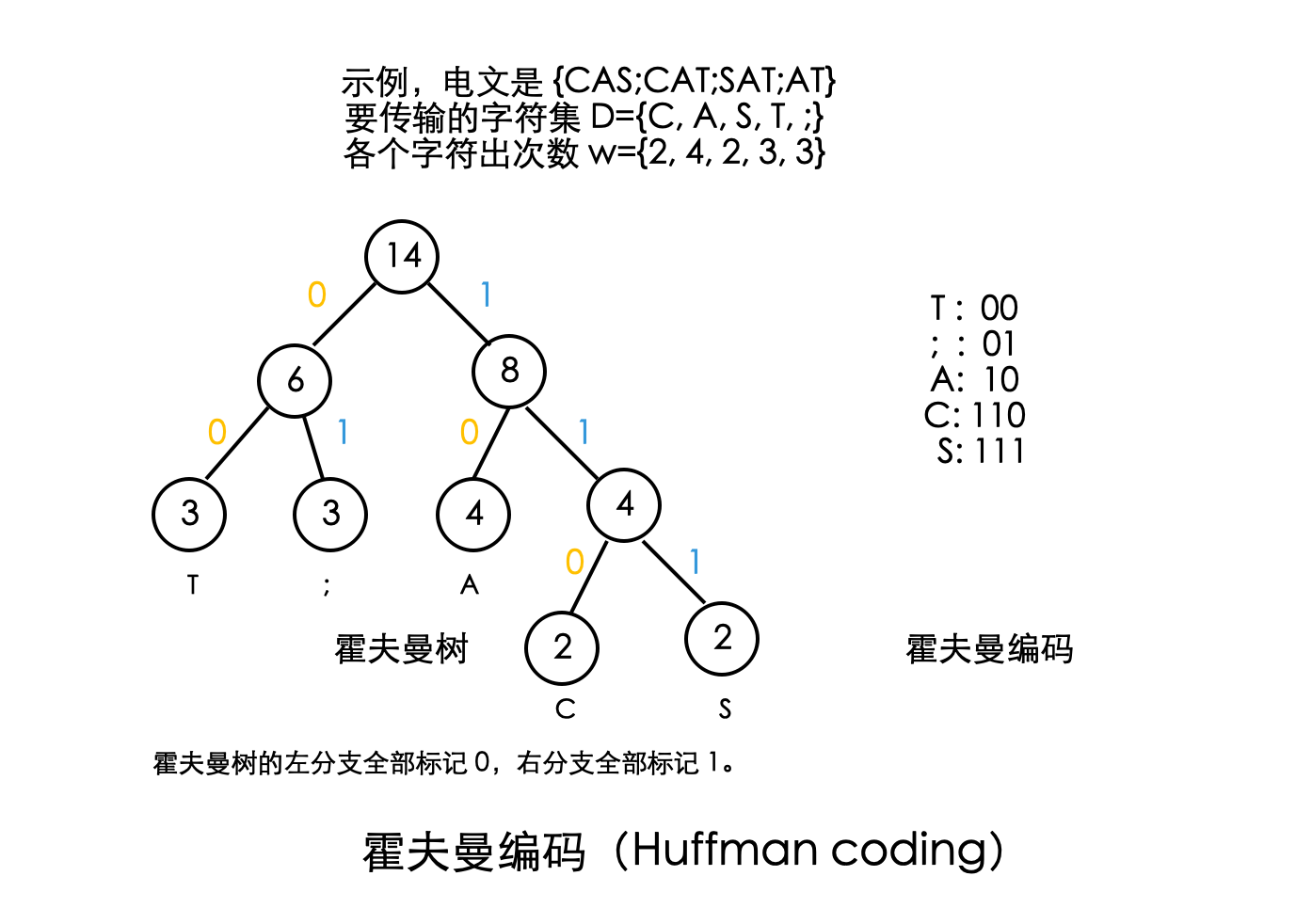
电文的霍夫曼编码为:11010111011101000011111000011000。这个编码有且只有一种解码方式,即 {CAS;CAT;SAT;AT}。霍夫曼编码是最优前缀编码,即字符编码的总长度最短。
QA
Q1: 为什么说霍夫曼编码是前缀编码?
因为没有一个叶子节点是另一个叶子节点的祖先,所以每个叶子节点的编码就不可能是其它叶子节点编码的前缀。
Q2: 为什么霍夫曼编码是最优前缀编码?
因为霍夫曼树的带权路径长度最短,故字符编码的总长度最短。
Q3: 同一字符集的霍夫曼编码只有一种吗?
不是,如果存在相同权重的节点,则取决于具体 select 函数的实现。
Q4: 无损压缩算法存在极限吗?
信息论 中说明了,无论使用什么压缩方法,文件大小都无法低于一个下界。一个直观的例子:压缩后得到的 zip 文件会比源文件更小,但一直重复压缩同一个文件并不会让文件大小变成 0,因为源文件终究含有一定量的信息。